杂耍算法及其证明

    这是编程珠玑上面的一个题，也是笔试中出烂了的题目。题目非常简单，描述如下：将一个n元一维向量向左旋转i个位置，例如当n=8，i=3时，向量abcdefgh旋转为defghabc。简单的代码使用一个n元的中间向量在n步内完成该工作。你能否仅使用额外字节的存储空间，在正比于n的时间内完成向量的旋转？

    下面是最简单的一种解法。

	#include <iostream>

	using namespace std;
	
	void reverse(char *a,int beg, int end)
	{
		char tmp;
		for (; beg < end; beg++, end-- )
		{
			tmp = a[beg];
			a[beg] = a[end];
			a[end] = tmp;
	    }
	}
	
	void LeftReverse(char *a,int n, int k)
	{
	     reverse(a,0,k - 1);
	     reverse(a,k,n - 1 );
	     reverse(a,0,n - 1);
	}
	
	int main()
	{
	     char test[] = "123abcdefg" ;
	     LeftReverse(test,strlen(test),3);
	     printf( "reversed:%s",test);
	     return 0;
	}

    当然，今天的主题不是这个，而是书中提到的另一种解法：英文是啥给忘了，翻译成“杂耍算法”。这个算法的步骤是这样的：move x[0] to the temporary t, then move x[i] to x[0], x[2i] to x[i], and so on, until we come back to taking an element from x[0], at which point we instead take the element from t and stop the process. If that process didn’t move all the elements , then we start over at x[1], and continue until we move all the elements.具体代码如下：

	#include <iostream>
	
	using namespace std;
	
	int gcd(int a,int b)
	{
	    int c;
	    if (a < b)
	    {
	        c = a;
	        a = b;
	        b = c;
	    }
	    while(b)
	    {
	        if(a % b == 0)
	            return b;
	        else
	        {
	            c = a % b;
	            a = b;
	            b = c;
	        }
	    }
	}
	
	void rotate(char * a,int n, int k)
	{
	    char tmp;
	    int j;
	    for (int i = 0; i < gcd(n,k); ++i)
	    {
	        tmp = a[i];
	        for (j = i + k; j!= i; j = (j + k) % n)
	        {
	            a[(j-k+n) % n] = a[j];
	        }
	        j = (j - k + n ) % n;
	        a[j] = tmp;
	    }
	}
	int main()
	{
	    char a[] = "abc12345678" ;
	    cout << "gcd(11,3):" << gcd(11,3) << endl;
	    rotate(a,11,3);
	    printf ( "after rotate:%s\n",a);
	    return 0;
	}

经过如下图所示的步骤之后，就完成了移位，此例中i=3,n=11。

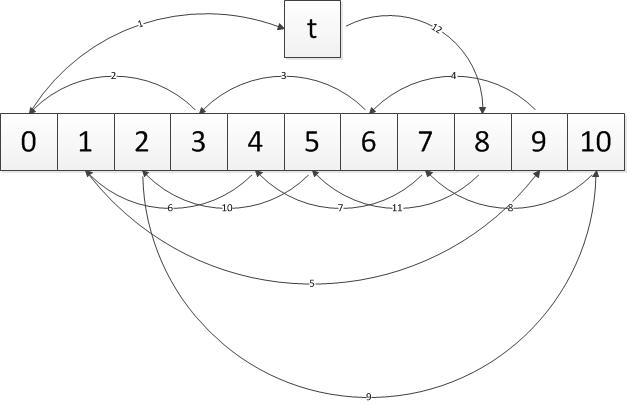
    这个算法会在执行\(gcd（i,n）\)次后就停止了，为什么？这就涉及到数论知识了，也就是今天的主题。

    数论中有这样一个结论：\(n\)个数

按照某种次序恰好组成\(\frac{n}{d}\)个数

的\(d\)份复制，其中\(d=gcd(i,n)\).例如，当\(n=12\)且\(i= 8\)时，有\(d=4\)，这些数就是\(0,8,4,0,8,4,0,8,4,0,8,4\).

    证明（指出我们得到前面\(\frac{n}{d}\)个值的\(d\)份复制）的第一部分是显然的，根据同余式的基本理论，我们有

可以看到当\(0\leqslant k< \frac{n}{d}\)时，我们得到了就是这\(\frac{n}{d}\)个数的\(d\)份复制，\(k\)的取值就是模数为\(\frac{n}{d}\)的最小完全非负剩余系中的数。

    现在证明这\(\frac{n}{d}\)个数就是\({0,d,2d,\cdots,n-d}\)（按照某种次序排列）。记\(i={i}'d,n={n}'d\).根据mod的分配率\(c(x\,mod\,y)=(cx)\,mod\,(cy)\),就有

所以当\(0\leqslant k< {n}'\)时出现的那些值就是\(d\)乘以以下诸数

我们知道\(({i}',{n}')=1\)，所以我们只需要证明\(d=1\)的情况，也就是\(i\)与\(n\)互素的情况。

现在我们假设\((i,n)=1\)，(1)式中的数是各不相同的，如若不然，取\(k,j\in [0,n-1],k\neq j\)，假设\(ki=ji\)，则有\(ki\equiv ji(mod\,n)\)。由于\((i,n)=1\)，则\(k\equiv j(mod\,n)\)，所以\(k=j\)，显然矛盾。所以(1)中的数恰好就是\(0,1,2,\cdots,n-1\)

    结论证完，下面回到例子简要分析，在本例中\(n=11,i=3,gcd(11,3)=1\)，于是

的值恰好就是\(11\)的最小非负完全剩余系按一定顺序 排列的结果。所以经过如下的步骤

t = x[0]
x[0] = x[i mod n]
x[i mod n] = x[2i mod n]
……
x[(n-2)*i mod n] = x[(n-1)*i mod n]
x[(n-1)*i mod n] = t

之后，所有的元素都到了该去的地方，

    当\((n,i)=d(d\neq 1)\)怎么办呢。从上面的结论我们可以知道每隔\({n}'=\frac{n}{d}\)之后，序列会从\(0,d,2d,\cdots,{n}'-d\)的某个序列重新开始，这样我们就又遇到\(x[0]\)了。这个时候我们需要将\(x[1]\)移到\(t\)，重复上述步骤，我们简要看看图示。

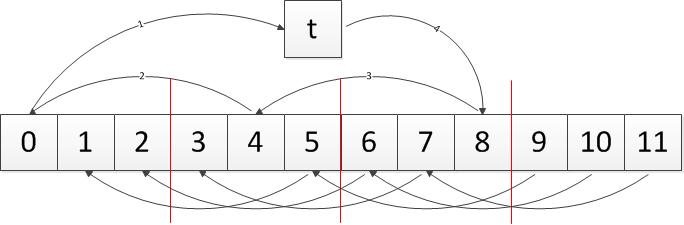
看看图示就明了了。

    这是复习数论的时候遇到的一个结论，然后想起曾经的一个题。现在确实是完全清晰了。人说，数学是科学的女皇，数论是数学的女皇，数论里面充满着迷人的结论。这世间充满了美妙，我希望能够与诸君分享。