回溯算法及其例子
源起
最近在看《算法》,其中有一个题是很老的问题,0~9入栈顺序一定,问哪些出栈顺序是不可能的。如0,1,2,…,7,8,9肯定是可以的,9,8,7,…3,2,1也可以,8,2,3,…就不可以。 这个问题本身是比较简单的,这个问题引出的问题就是求出所有可能的出栈顺序,主要是借此机会复习一下回溯法。
先来就题论题。解题的关键还是模拟出入栈,比如要判断的例子是4,3,2,1,0,9,8,7,6,5。我们先看到第一个出的是4,必然0,1,2,3已经依次压栈了。
-
我们首先建立一个空栈s,,还有一个输入序列的index,这表示出栈的值,以及即将入栈的元素in,index和in的初始值显然是0,input表示输入的序列;
-
当in不等于input[index]时,我们将in入栈,in再加1,直到其等于input[index];
-
in++,index++;这表示4已经顺利出栈;
-
然后比较s.peek()跟input[index]的值,如果不同,继续循环入栈,相同则出栈;
对照例子我们人肉走一遍程序:
-
in=0,input[0]=4,将0,1,2,3入栈s;
-
in=4时,in=input[0],接着in=5,index=1;
-
栈顶3与序列中input[index]相等,index=2;一直到0都相等;此时,index=5,in=5,栈s为空;
-
5小于9,将5,6,7,8入栈;
剩下的跟1~3步类似了。
代码如下:
public class StackSeq
{
public static boolean isOk(int[] input,int n)
{
int index = 0;
int in = 0;
Stack<Integer> s = new Stack<Integer>();
while(true)
{
if(index >= n - 1)
return true;
if(in >= n)
return false;
if(in != input[index])
{
s.push(in);
++in;
continue;
}
++in;
++index;
while(!s.isEmpty() && s.peek() == input[index])
{
++index;
s.pop();
}
}
}
public static void main(String[] args)
{
StdOut.println("input the number of arrays:");
int n = StdIn.readInt();
int[] input = new int[n];
while(true)
{
for (int i = 0 ; i < n ; ++i)
{
input[i] = StdIn.readInt();
}
boolean ret = isOk(input,n);
if(ret == true)
{
StdOut.println("the sequeue is ok!");
}
else
StdOut.println("the sequeue is not ok!");
}
}
}
原谅我那蹩脚的java。
回溯简介
知道了如何判断一个序列是否是正确的出栈序列,我们自然会想到求出所有的正确出栈序列。这也是本文的主题,回溯算法。回溯算法的思想还是比较简单,我在百度百科摘了一段如下:
从一条路往前走,能进则进,不能进则退回来,换一条路再试。八皇后问题就是回溯算法的典型,第一步按照顺序放一个皇后,然后第二步符合要求放第2个皇后,如果没有符合条件的位置符合要求,那么就要改变第一个皇后的位置,重新放第2个皇后的位置,直到找到符合条件的位置就可以了。回溯在迷宫搜索中使用很常见,就是这条路走不通,然后返回前一个路口,继续下一条路。回溯算法说白了就是穷举法。不过回溯算法使用剪枝函数,剪去一些不可能到达 最终状态(即答案状态)的节点,从而减少状态空间树节点的生成。回溯法是一个既带有系统性又带有跳跃性的的搜索算法。它在包含问题的所有解的解空间树中,按照深度优先的策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时,总是先判断该结点是否肯定不包含问题的解。如果肯定不包含,则跳过对以该结点为根的子树的系统搜索,逐层向其祖先结点回溯。否则,进入该子树,继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时,要回溯到根,且根结点的所有子树都已被搜索遍才结束。而回溯法在用来求问题的任一解时,只要搜索到问题的一个解就可以结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法,它适用于解一些组合数较大的问题。
我在网上找到了这里有一个比较好的说明。这里我们用求1,2,3…n数里面r个数的排列来简要介绍一下回溯算法。在上面的链接中偷了一张图
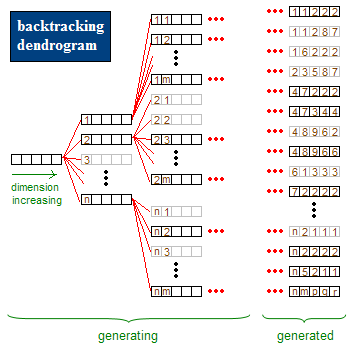
也就是第一步的时候我们选择1——n中一个数,比如选了1,然后再在剩下的n-1个数中求出其排列,完了,我们再回溯到第一步,选择2,之后的依此类推。为了不产生重复的数字,我们在进行下一步的前进之前进行了判断。代码如下:
#include <iostream>
using namespace std;
int count = 0;
void print(int* a,int m)
{
for (int k = 0; k < m; ++k)
{
cout << a[k] << " ";
}
cout << endl;
}
void tuple(int* a,int i,int m,int n)
{
if(i == m)
{
print(a,m);
count++;
return;
}
for (int k = 1; k <= n; ++k)
{
for (int h = 0; h < i; ++h)
{
if(a[h] == k)
{
goto LOOP;
}
}
a[i] = k;
tuple(a,i+1,m,n);
LOOP:
continue;
}
}
int main()
{
int a[1000];
int n,m;
cout << "input C(n,m) :\n";
cin >> n >> m;
cout << "("<< n <<","<< m << ")排列数" << endl;
tuple(a,0,m,n);
}
根据这段代码求组合数跟全排列也很简单了。总结一下使用递归解回溯,递归函数第一部分判断递归终止条件,然后是递归进入下一个维度,之后回溯。
所有可能出栈顺序
我们来看看这个问题如何使用回溯法。
关键的点就在,“一个元素i入栈之后,我们面临两种选择,i出栈,或者i+1入栈”,这就有了回溯的基础。而问题的终点就是有了N个元素之后。递归函数就应该这样设计
public static void printiter(int n,int cur,Stack<Integer> tmp,Vector<Integer> out)
n是元素个数,解的维度,cur表示当前的维度,tmp表示2中选择中的进栈,out存放的出栈的元素。终止条件显然是out的元素个数是n。得源码如下:
public static void printiter(int n,int cur,Stack<Integer> tmp,Vector<Integer> out)
{
if(n == out.size())
{
for(int i : out)
{
StdOut.print(i + " ");
}
StdOut.println("");
count++;
return;
}
if(cur != n)//入栈
{
tmp.push(cur);
printiter(n,cur + 1,tmp,out);
tmp.pop();
}
if(!tmp.isEmpty())
{
int x = tmp.pop();
out.add(x);
printiter(n,cur,tmp,out);
out.remove(out.size() - 1);
tmp.push(x);
}
}
八皇后问题
借这个机会再来说说八皇后这个老问题。8*8的棋盘上放8只皇后,使得每一只都不相互攻击对方。我们一步一步用上面的思路来解决这个问题。容易想到使用
bool solution[7][7]
来表示每个位置的是否放皇后,如果为false则不妨,true就放皇后。我们首先可以得出如下的结构,能够将所有的可能计算出来。
#include <iostream>
using namespace std;
#define N 8
bool solution[N][N] = {false};
void print_solution()
{
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
cout << solution[i][j] <<" ";
}
cout << endl;
}
cout << "\n\n\n";
}
void QueenIter(int x,int y)
{
if(y == N)
{
x++;
y = 0;
}
if(x == N)
{
print_solution();
return;
}
solution[x][y] = true;
QueenIter(x,y+1);
solution[x][y] = false;
QueenIter(x,y+1);
}
int main()
{
QueenIter(0,0);
}
看出结构也是首先判断是否终止,然后遍历该维度能取得所有值,进入下一个维度。(该例输出太大,若要跑程序,建议将N改成4)
下面的步骤是排除所有不可能的解,很明显只有当要放皇后的时候才需要判断。
我们建立4个bool数组,数组中的每个元素记录这个位置还能否放皇后。为了使得皇后的个数为8,我们还需要增加一个参数c,只有c等于8时,我们才输出方案。
void QueenIter(int x,int y,int c)
{
if(y == N)
{
x++;
y = 0;
}
if(x == N)
{
if(c==N)
{
print_solution();
}
return;
}
int d1 = (x+y) % 15;
int d2 = (x-y + 15) % 15;
if(!mx[x] && !my[y] && !md1[d1] && !md2[d2])
{
mx[x] = my[y] = md1[d1] = md2[d2] = true;
solution[x][y] = true;
QueenIter(x,y+1,c+1);
mx[x] = my[y] = md1[d1] = md2[d2] = false;
}
solution[x][y] = false;
QueenIter(x,y+1,c);
}
由于一行只能放置1个皇后,可以改进一下,改进后如下:
#include <iostream>
using namespace std;
#define N 8
int solution[N] = {0};
bool my[8],md1[15],md2[15];
int count = 0;
void print_solution()
{
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < solution[i]; ++j)
{
cout << 0 << " ";
}
cout << 1 << " ";
for (int j = solution[i] + 1; j < N; ++j)
{
cout << 0 << " ";
}
cout << endl;
}
cout << "\n\n\n";
}
void Queen(int x)
{
if(x == 8)
{
print_solution();
count++;
return;
}
for (int i = 0; i < N; ++i)
{
int d1 = (x+i) % 15;
int d2 = (x-i+15) % 15;
if (!my[i] && !md1[d1] && !md2[d2])
{
my[i] = md1[d1] = md2[d2] = true;
solution[x] = i;
Queen(x+1);
my[i] = md1[d1] = md2[d2] = false;
}
}
}
int main()
{
Queen(0);
cout << count << endl;
}
blog comments powered by Disqus